
娘「パパ~、ガチャガチャやりたい」
ぼく「おっ、いいよ。そういえばひさしぶりな気がするし」
娘・息子「やった~!」
ぼく「はい、じゃあひとり300円ね」
息子「パパもなんかやったら?」
ぼく「うーん、たしかに。なんかいいのあったらやってみようかな。初代キン消しとか」
残念ながら初代キン消しは32年前に販売終了していたので買えなかったのだが、かわりに見つけたのが……


『ポケモン ぺたんこマスコット Type:でんき』だ!
かわいい~! しかも1個200円! いまどきのガチャにしては安い!

ええっと、ラインナップは、ピカチュウ、ピチュー、モルペコ(まんぷくもよう)、モルペコ(はらぺこもよう)、コイル、バチンウニか。
どれも好きなポケモンだが……

ぼくはモルペコグッズに目がないモルペコ大好き人間なので、2種のモルペコのうちどちらかは出てほしい。
ぼく「ええっと、このラインナップだとモルペコは6分の2だから、2回引けばどっちかは当たるかな、たぶん」
娘「えっ、なんで!?」
ぼく「確率で言うと、2回引いてモルペコが1回も出ない確率は9分の4だから、えーっと、9分の4ってだいたい44%くらいだから、モルペコが1回以上出る確率の56%のほうが高いからだよ」
娘「ええ~!? なにそれ!? どういうけいさんでわかるの!? ちゃんとおしえて!」
うーん。確率を習うのって、小学校高学年だっけ? 中学校だっけ?
いずれにせよ、小学校低学年が理解するのって、けっこう難しそうな気がする……娘も息子も、ポケモンのわざの命中率など、ゲームの世界で確率には頻繁に触れているとは言え……
まあ、いいか。興味があるのはいいことだ。
かくして、ガシャポン売場のすみっこで、娘・息子を招集しての簡易確率講座が始まった。

ぼく「まず、6種類のうち2種類がモルペコ。このどっちかを引きたい。これはつまり、中身に偏りがなければ、当たりが『6分の2』入っていると言うことができます」
娘「なんで?」
息子「6こあるうちの、2こだからでしょ?」
ぼく「そうです! すばらしい。そして逆に言うと、モルペコが出ないのは『6分の4』です」
娘「あ~、6こあるうちの、4こだからだ」
ぼく「すばらしい! となると、1回だけ買うと、モルペコが出ない確率のほうが高いのはわかる?」
娘・息子「わかる!」
ぼく「この6分の4は、『4÷6』とも言うことができます。これをすると、『0.6666…』となって、要はまあ、だいたい67%です。67%の確率でモルペコじゃないのが出てくる、となります」
娘「まんなかよりたかいね」
息子「かみなりのめいちゅうりつくらいだ」
さすがふたりとも、ゲームで鍛えられているだけのことはあるな。習ったわけでもないのに、67%と聞いて「やや高い」ということが直感的にわかるのはすごい。
世の中に多数いる「99%は低い、信用できない」とすぐ言い出すファイアーエムブレムおじさんやスパロボおじさんに聞かせてあげたい。まあ、ぼくのことなんだけど。

ぼく「で、モルペコが出ない確率と、モルペコが出ない確率をかけ算すると、2回やってもモルペコが出ない確率が出てきます。これは何%と読むでしょう」
息子「44パーセント!」
ぼく「すばらしい! 44パーセントです。まんなかよりちょっと低いね。つまり……?」
娘「モルペコがでるかくりつのほうが、たかい!」
ぼく「大正解! おめでとう! モルペコが出る確率は56%もあります!」
まあ、厳密に言えばガシャポンマシンに入っているカプセルは有限だし偏りもありうるので正しくない部分もあるのだが、おおまかな確率計算としては上記で間違いない。
しかし、娘も息子も理解が早くてすごいな。ゲームやガシャポンは教育にいいな。

よし、実演だ! 回していくぞ!
2回引く予定だが、1回目の結果は……
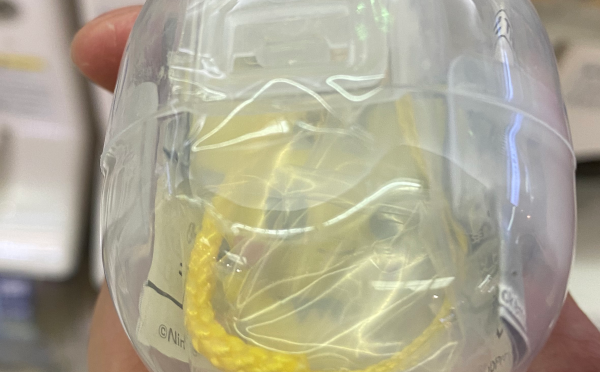
……
ピチューだな、これは……
息子「あれ? ピチュー?」
ぼく「ピチューだね。まあ、いきなりモルペコは来ないでしょ。ある意味、確率通りだよ」
娘「かくりつってすごいな~。これって、ピチューがつづけてでちゃうかくりつもわかるの?」
ぼく「おっ、いい疑問だね。わかるよ。6分の1が2回だから、36分の1で……3%くらいしかないんじゃないかな、たぶん。ほぼあり得ない確率だよ」
娘「え~、ひくっ! じゃあ、つぎはモルペコがでるね、きっと」
まあ、厳密に言うとすでにピチューを引いてしまったいま、ここからピチューを引く確率は6分の1あるのだが、全体で見れば、子どもたちに説明した通り36分の1で間違いない。
ぼく「こんな感じで、算数とか数学とかはね、こういうガチャとかゲームとかではけっこう役立つんだよ。勉強しとくといろいろ使えるよ」
息子「パパあたまいい~!」
娘「がっこうのせんせいみたい!」
感心してもらえたようで、よかった。小さなことだが、うれしいことだ。
ぼくは彼らに、こういう学校以外の学びの場を大切にしてほしいな、と思う。遊びと学びをリンクさせて、楽しみながら成長していってほしいな、と願う。

いまもこうして、ぼくがガチャを2回引く姿を通して、彼らは「確率」というものへの理解がずいぶん進んだはずだ。
授業料たったの400円。しかも、ピチューとモルペコのマスコットまで手に入る。
これは安いどころか、おつりが来るレベルの投資だとぼくは思って

ピチューじゃねーか!!




コメント
確率はあくまで確率でしかないという良い勉強になったね
どこかのむちむちゲーで資材溶かしてる人にも聞かせてあげたい
確率の厳しさも教えている素晴らしい反面教師ですね!!
99%が信用できない→1%は引ける→ピチュー2連続とお手本を示していく
ちゃんと出るまで引けば実質無料ってことまで教育してあげて
出るか出ないかの2分の1論を推していけ
かみなりの命中率と同じくらいってすぐ置き換えできるの天才では?
なんか素敵子ども産みたくなった
ポケモンならないだろうけどガチャガチャには不均一アソートっていう罠が存在するから気をつけたほうがいい。昔仮面ライダーのガチャガチャで疾風と切り札は1台に一個ずつ メタルとトリガーは一台に2個ずつしか入ってない奴があってサイクロンばっかりアホみたいに出た
理屈は正しいが結果は最悪な事でおなじみのゲムぼく。
反面教師の例として教科書に乗って欲しい
「父親」としては本当に素晴らしい御方。ドスケベ界では異端児でいらっしゃって…。
比較的まともな記事が2日続いたのでそろそろ反動でドスケベスキンフェスティバルが来そう
オチはわかってたのに実際ピチュー2連続の画像を見たら大笑いしてしまった。悔しい
昨日の記事ならダビスタ案件が、今日の記事ならポケモン案件が来る可能性もある…かもしれないけど、いい話が続いたから明日の記事でまた新規をフルイに掛けにくるんだろうな。ラスオリの新スキンも実装されたし…
魔法の言葉 出るまで引けば100%
アーエム警察もニッコリ
まぁ実際のガチャポンって人気キャラ少なくしたり塗装工数多そうなの少なかったりするしね…
物理ガチャは筐体内が一杯ならよっぽどなことがない限りコンプできるからマシ。
FEおじさん「99%は信用できない」
ソシャゲおじさん「1%なら全然引ける」
確率って面白いねえ
いきなりベンダーを横から覗くおじさんにならなくてよかった
スマホのライトで筐体内照らして次の出玉覗いたりしてなくて良かった。
たとえ最初は均一に入っていたとしても他の人が引いて偏りが出ている可能性もあるんだよね…
うるっときてしまった
明日来るであろうスケベ記事を待っています。
↑
他の人が引いてても、「他の人がモルペコを引く確率」は同じだから、見えてない限り同じだよ
◯と×しかないクジで考えてみたらいい
前の客が◯を引いていたら◯を引く確率は0%だけど、前の客が◯を引く確率は50%なので、自分が◯を引く確率は相手が◯を引いてない確率=50%。
つまり、クジは先手でも後手でも確率は変わらない
(一番くじのように引かれたクジを確認して引ける場合はその限りではない、が、やはり引ける確率で言えば同じ)
序盤に賢いゲムぼくさんが出てくると成功率がグッと下がるイメージ
そもそもパーセンテージがちゃんと100%基準で話進んでるのすごくね?
たまにでてくるゲムぼくお父さん好き
結果のパターンだけが分かってて内部の分布がわからなければ何回引いても確率は変わらないのが正解だと分からせてくれる良い記事
騙されたお子さんたちは可哀想なのでなんか補填してやれ
56%なら大体引けるだろって考えるなんて、ポジティブなんだねゲムぼくさん
100%じゃないなら0%みたいなもんだろおじさんかと思ってたよ
期待していたオチがキタ!
IQゼロになって引いたブルアカのガチャはノノミもワカモの引けたのに
まともな時は引けないの、神がIQゼロを望んでる証拠だよ
別のガチャだけど
全11種で目当てのやつが26回目でようやっと引けた
まあ偏りすぎだな
ネタとしては100点満点のオチだけど
借金おじさんのなけなしの400円だと思うと悲しいな
がっつり確立習うのは高校数学だからお子さんたちかなり優秀やで。
踏み込みが足りん!
条件付き確率まで理解できてて偉い
信用していい確率は0か100だけだ
オチが美しい良記事
オチとしてもきれいだし、確率すり抜けに絶対ナイは無いということがよくわかるいい記事だ
これで倒せる時の命中99%のアーチャーが攻撃を外した時!
あと一回攻撃当てれば闘技場勝ち抜きの時に敵ソードマスターに必殺1%引かれた時!
そうやっておじさん達は大人になっていった!
3%は起こりそうに無いと感覚的には思うけど、実は稀によくあるという確率感覚を身銭を切って実演するとは、なかなかできんぜ。
ファイアーエムブレムのせいで100%以外の確率は0%と同じとみなすようになったけどおかげでギャンブルにははまらずにすみました
ガチャ要素あるんでハチナイはやめます
これは敵ソドマスの必殺引いてますわ
補充する時バラけさすの面倒で〇〇3個ドバー、△△4個ドバーとかしてごめんね
1%だろうと3%だろうと当たるときは当たる
逆もまた然り
これが生きた教育って奴だな
スパロボおじさんよりコイルのほうが好き
自分だけ300円をオーバーしてて草